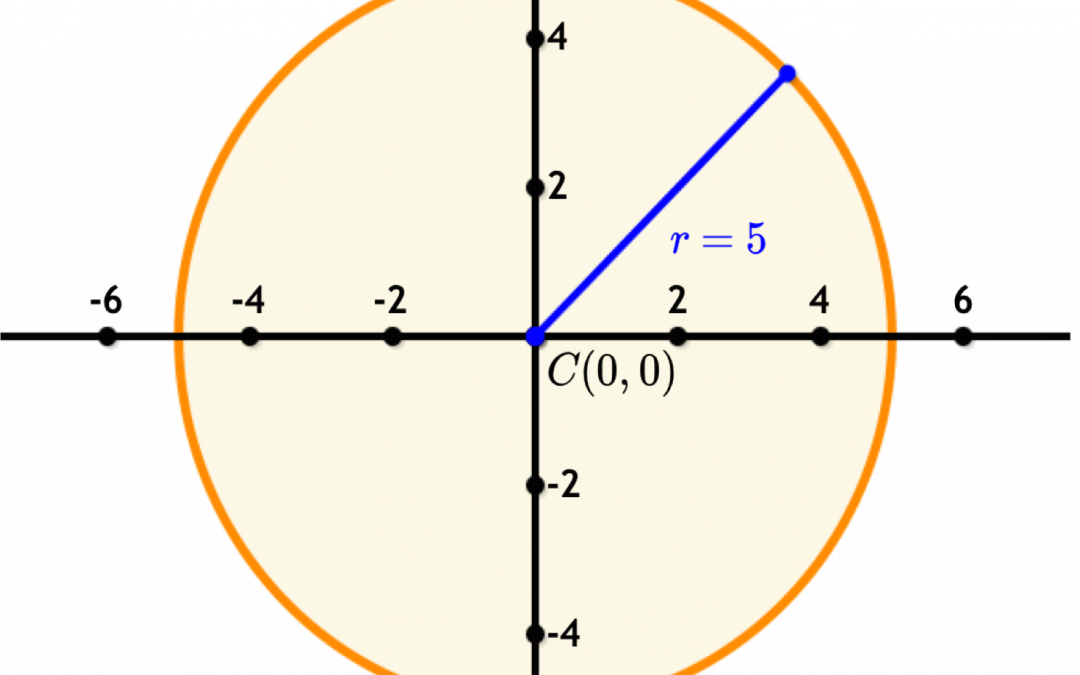
Need a higher SAT Math score? The best book for SAT Math prep covers the Equation of a Circle in detail and exactly how it’s tested on the SAT Math test - with tons of practice and detailed explanations.
The Equation of a Circle
Pretty much every SAT has one or two questions dealing with the equation of a circle. As such, it’s important for students to be prepared to encounter problems testing them on the equation of a circle. Yet most students aren’t aware exactly WHAT the standard form for the equation of a circle is. To make matters more complicated, often the SAT gives students circle equation problems in which the equation is NOT in the normal form, and students need to know how to put it in that form to allow themselves to correctly answer questions on the equation of a circle. Today, we’ll take a look at the equation of a circle and do some real SAT problems testing you on this concept.
Memorize This Equation
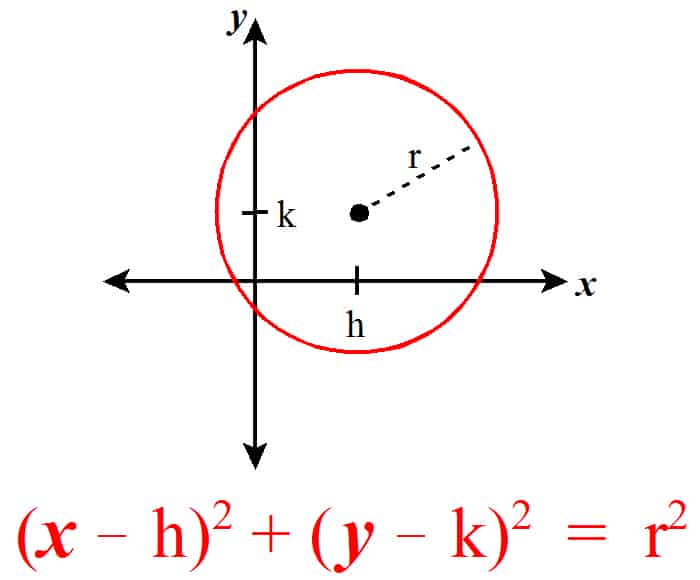
There it is! X minus H squared plus Y minus K squared equals R squared. Remember it! And be ready to recognize when circle equations ARE in the form and when they’re not. Let’s go over what the equation of a circle means.
X is the x variable. Y is the y variable.
The point (h,k) is the coordinate point of the CENTER of the circle.
R is the radius of the circle. Notice that in the standard form of the equation of a circle, you need the CENTER and the RADIUS SQUARED.
Also notice that X minus H squared and Y minus K squared are perfect squares.
What if the Equation Isn’t in Standard Form?
If you have something like….
x^2 + 20x + y^2 +16y = -20
…notice it is NOT in the standard form. X^2 + 20x and y^2+16y are NOT perfect squares, so if you want to figure out what the center or the radius of the circle is, you’ll need to put the equation in standard form. How do you do that? It’s called completing the square.
Completing the Square
Luckily, completing the square is pretty easy if you memorize what to do. Let’s go through the steps, working with the above equation, to put the circle into standard form so that the center of the circle and the radius of the circle reveal themselves.
1) Group your terms together
This basically means to put the x squared term and the x term next to each other and the y squared term and the y term next to each other. That’s already done for you in the above equation.
2) Add and subtract the square of half of the x term. (Do the same for the y term, as the circle equation has two squares we need to complete.)
This phrase is THE phrase to memorize when it comes to completing the square. There is no substitute for memorization, unforunately. If you’re the type of student who learns a formula or learns a concept only to forget it the next day, you’re going to have a difficult time on the SAT. A tutor can tell you the concepts and formulas you need, but if YOU don’t memorize them, you will find yourself out of luck. So memorize how to complete the square. Anyway, let’s look at what “Add and subtract the square of half of the x term” means.
(x^2 + 20x + 100) - 100 + (y^2 +16y + 64) - 64 = -20
Notice what we did. We saw that the x term was 20, so first we took half of that, which is 10, and then we squared it, making 100. Then we added AND subtracted 100 to the left side of the equation. Why add something just to immediately subtract it? Because you can’t randomly add something to an equation. You’d change its value. So we basically added 0 but changed what the equation LOOKED like.
Look what we produced! We now have 2 perfect squares ready to FACTOR.
3) Factor
(x+10)^2 -100 + (y+8)^2 - 64 = -20
Notice we still have our minus 100 and our minus 64 on the left side. But in the standard form of the equation of a circle, that extra stuff isn’t there. That means we need to send it to the right side of the equation by adding it to both sides. Watch.
(x+10)^2 + (y+8)^2 = 144
That’s it! Now it’s in the standard form. Its value didn’t change at all. It’s still the same circle, the same equation, just in a different form. Now that we have the equation of the circle in standard form, we’re ready to interpret it.
What’s the center of this circle?
It’s (-10, -8)
And what’s the radius? It’s 12.
This is problem 29 in the calculator math section of Practice Test #5. One of the tricky problems. But like ALL tricky problems, if you know how to solve it, it’s quick and easy.
So What Are the Takeaways?
First, you need to memorize the standard form of the equation of a circle. X minus H squared plus Y minus K squared equals R squared. Second, you need to know what the equation represents. (H,K) is the center of the circle, and R is the radius. Third, you need to know how to complete the square in case the circle is NOT in standard form already. To do that, add and subtract the square of half of the X term and factor!
If you want more practice with Equation of a Circle questions on the SAT Math test, you need our textbook SAT Math Mastery Vol.2. You’ll never think this topic is hard again! Order it on Amazon or learn more about it here.
Good luck on the SAT 🙂
* * *
That’s it! For even more great SAT and ACT prep tips, check out the rest of our blog. Looking for 1-on-1 ACT or SAT prep tutoring to help you with the college application process? Want to join an SAT or ACT group class? Contact us today! We’re perfect-scoring tutors with years of experience helping students achieve the SAT and ACT scores they need to make their dreams a reality!